Bir graph’ın tüm vertex’leri üzerinde gezinme işlemine traversel denilmektedir.
Gezinme işlemi için kullanılan iki temel algoritma:
- Breadth First Search (Genişlik Öncelikli Arama)
- Depth First Search (Derinlik Öncelikli Arama)
dır.
Breadth First Search – BFS (Genişlik Öncelikli Arama)
Bir başlangıç vertex’inin belirlenip önce o vertex’in komşuları, sonra komşularının komşularının ziyaret edildiği queue veri yapısından faydalanılan gezinme yöntemidir.
İlk önce bir başlangıç vertex’i belirlenir ve ve kuyruğa atılır. Daha sonra o vertex’in komşuları kuyruğa atılır. Kendisi ziyaret edildi olarak işaretlenir ve kuyruktan çıkarılır. Bu işlem kuyrukta eleman bitene kadar yani tüm vertex’ler gezilene kadar devam eder. Eğer bir vertex daha önce ziyaret edildi olarak işaretlendiyse veya kuyruğa atıldıysa, tekrar kuyruğa atılmaz.
Aşağıdaki graph’ı bread first search ile gezip spanning tree oluşturalım.

Başlangıç vertex’i “A” olsun. A’nın komşularını kuyruğa ve ağaca ekleyelim. Kendisini ziyaret edildi olarak işaretleyelim.

Sıradaki “B” vertex’ine geçelim. Komşularını kuyruğa ve ağaca ekleyelim. A ve G daha önce kuyruğa eklendiği için tekrar eklenmeyecek. B vertex’ini ziyaret edildi olarak işaretleyip kuyruktan çıkaralım.
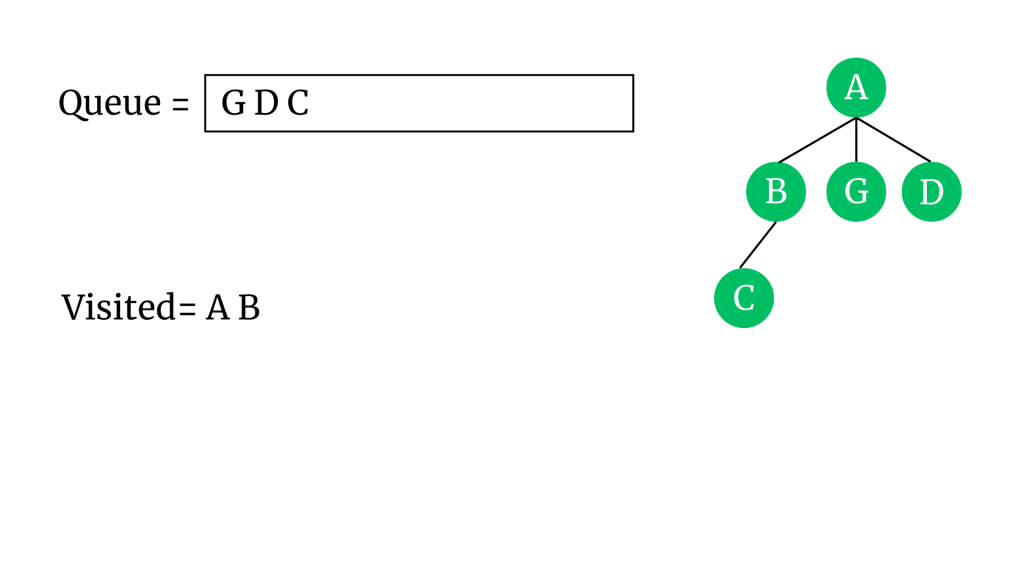
“G” vertex’inin komşusu H’yi kuyruğa ve ağaca ekleyelim. G vertex’ini ziyaret edidi olarak işaretleyip kuyruktan çıkaralım.
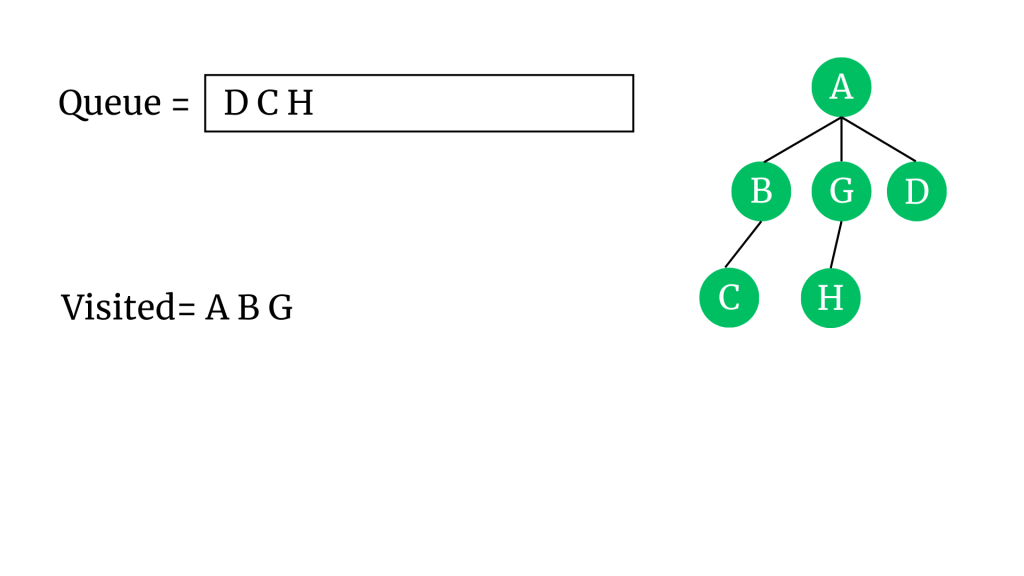
“D” vertex’inin komşusu olan F’yi kuyruğa ve ağaca ekleyelim. D’yi ziyaret edildi olarak işaretleyip kuyruktan çıkaralım.
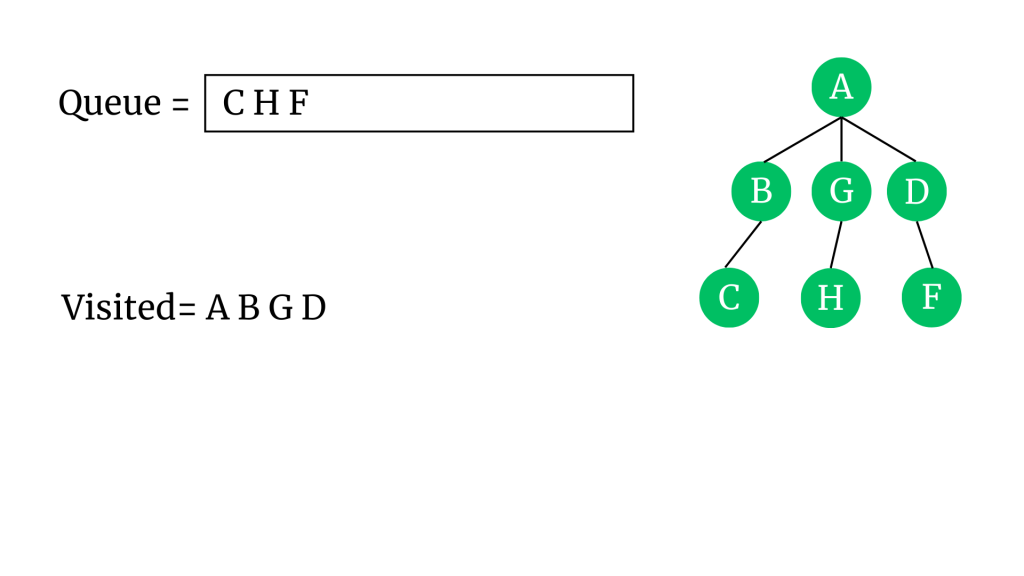
“C” vertex’inin komşusu olan E’yi kuyruğa ve ağaca ekleyelim. C’yi ziyaret edildi olarak işaretleyip kuyruktan çıkaralım.
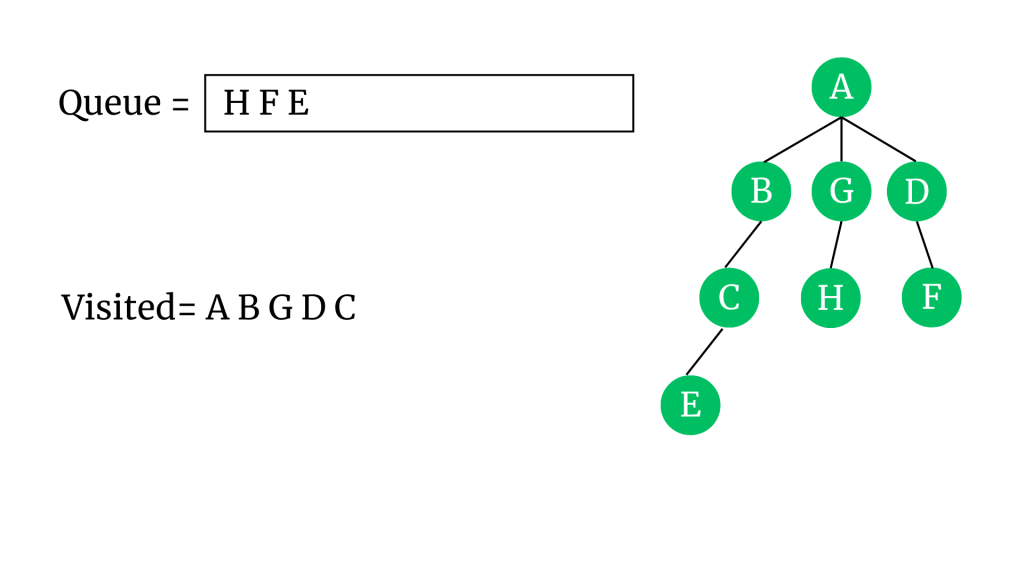
“H” vertex’inin komşusu olan K’yi kuyruğa ve ağaca ekleyelim. H’yi ziyaret edildi olarak işaretleyip kuyruktan çıkaralım.
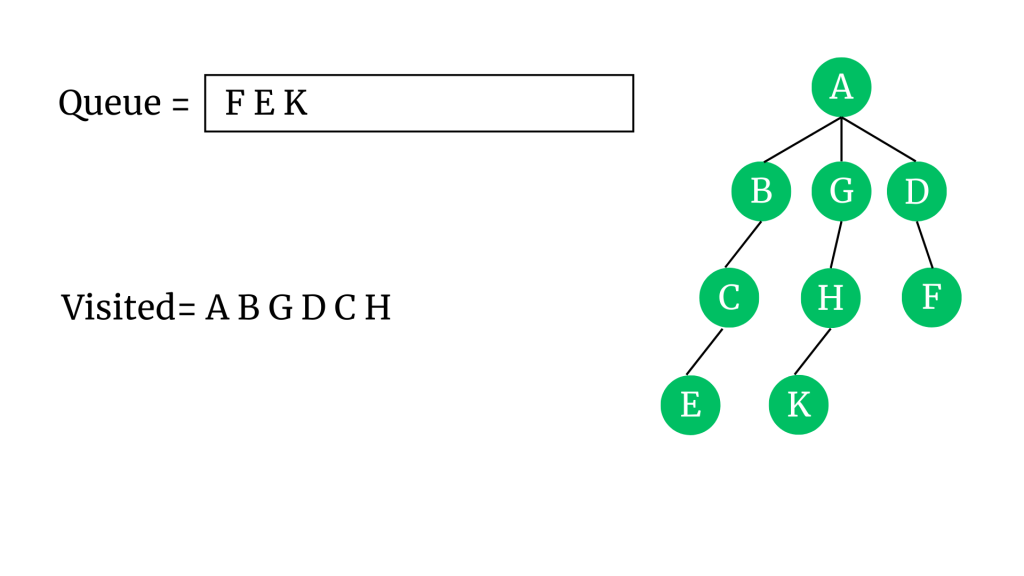
Sıradaki “F” vertex’ine geçelim. F vertex’inin komşuları ya ziyaret edildiğinden ya da şu anda kuyrukta bulunduğundan hiç bir komşusunu kuyruğa ekleyemiyoruz. F’yi ziyaret edildi olarak işaretleyip kuyruktan çıkaralım.
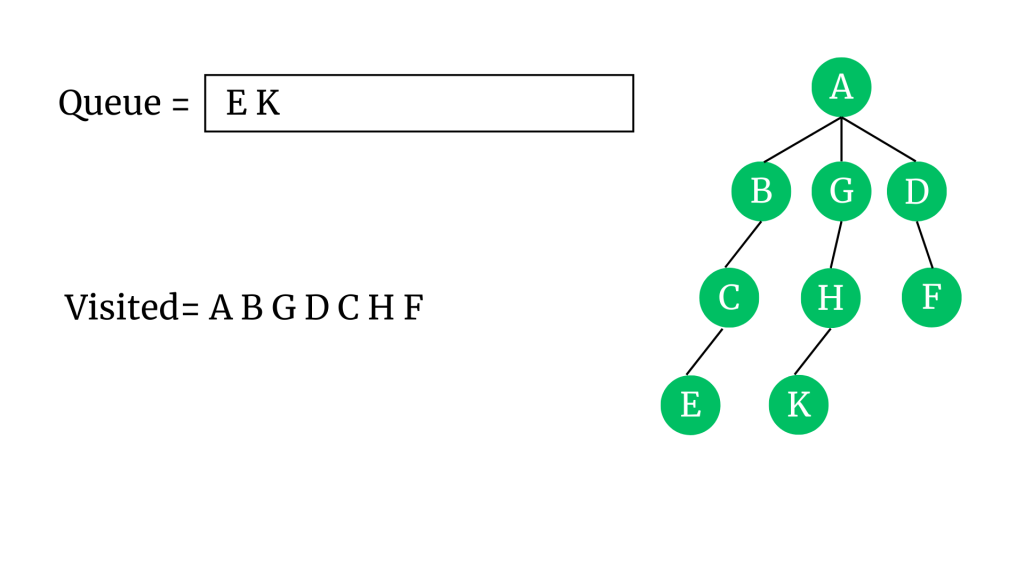
E’nin kuyruğa ekleyebileceğimiz komşusu yok. Kendisini ziyaret edildi olarak işaretleyip kuyruktan çıkaralım. Yine K’nin de kuyruğa ekleyebileceğimiz komşusu yok. K’yi ziyaret edildi olarak işaretleyelim.
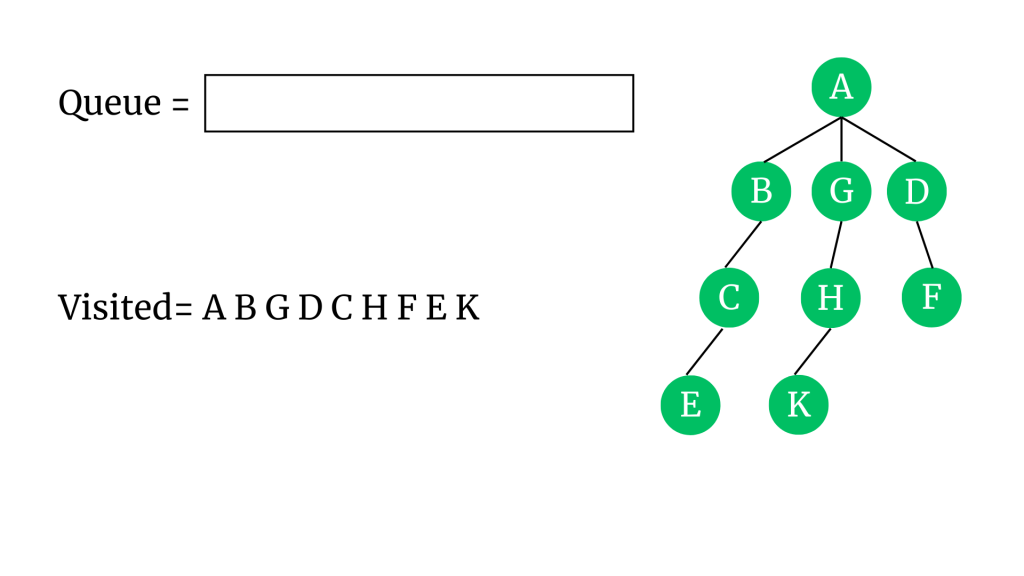
Tüm vertex’ler ziyaret edildi ve kuyruk boşaltıldı. Böylece graph’da BFS ile gezinme işlemi tamamlandı.
Depth First Search – DFS (Derinlik Öncelikli Arama)
Bir başlangıç vertex’inin kenarından gidilebilecek en uzak vertex’e kadar gidilen, stack veri yapsından faydalanılan gezinme yöntemidir.
İlk olarak bir başlangıç vertex’i belirlenir ve ziyaret edildi olarak işaretlenir. O vertex’in komşuları stack’a atılır. Stack’deki top eleman için bu işlem tekrarlanır. Bu işlem stack’de eleman bitene kadar yani tüm vertex’ler gezilene kadar devam eder.
Aşağıdaki graph’ı depth first search ile gezip spanning tree oluşturalım.
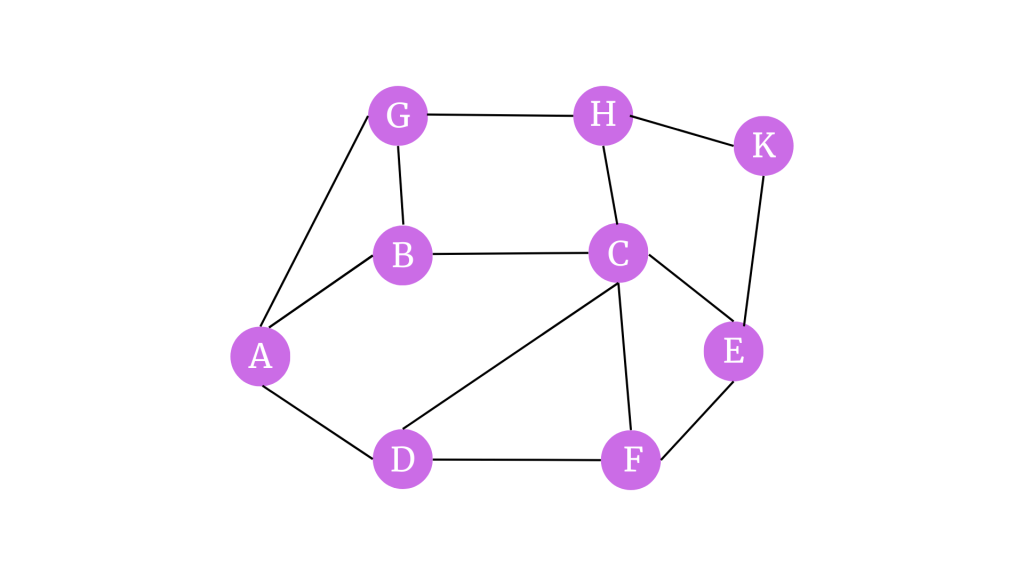
Başlangıç vertex’i “A” olsun. A’nın komşularını stack’e ekleyelim. A’yı ziyaret edildi olarak işaretleyip ağaca ekleyelim.
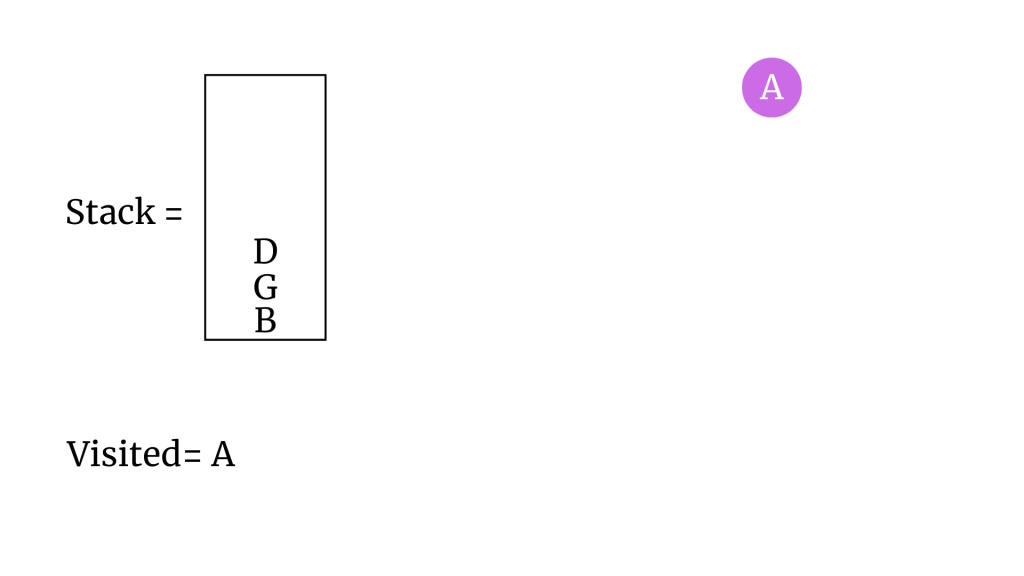
“D” vertex’nin komşularını stack’a ekleyelim. D’yi ziyaret edildi olarak işaretleyelim ve stack’tan çıkaralım. D’yi ağaca ekleyelim.
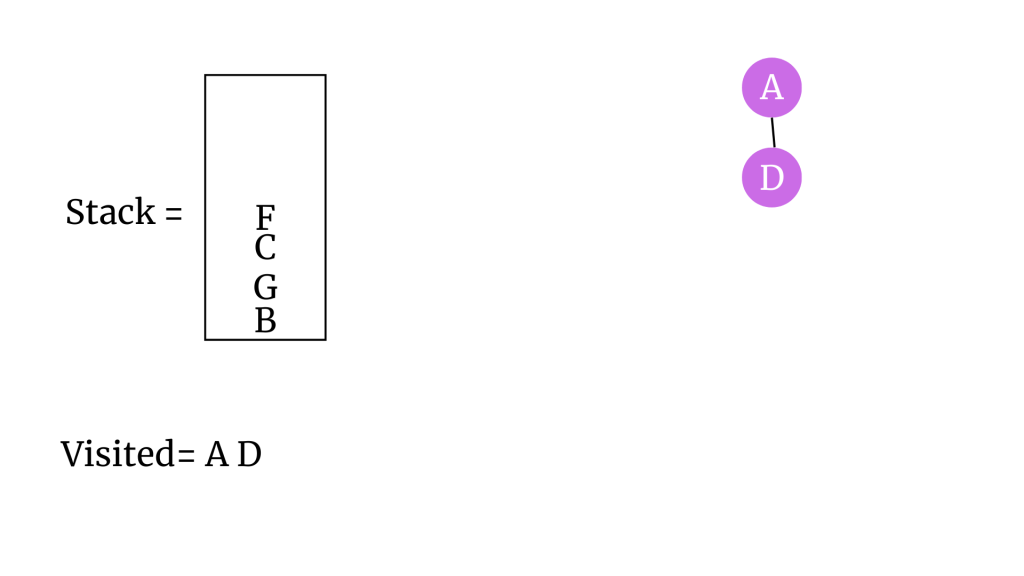
“F” vertex’inin komşusu olan E’yi stack’e ekleyelim. F’yi ziyaret edildi olarak işaretleyelim ve stack’ten çıkaralım. F’yi ağaca ekleyelim.
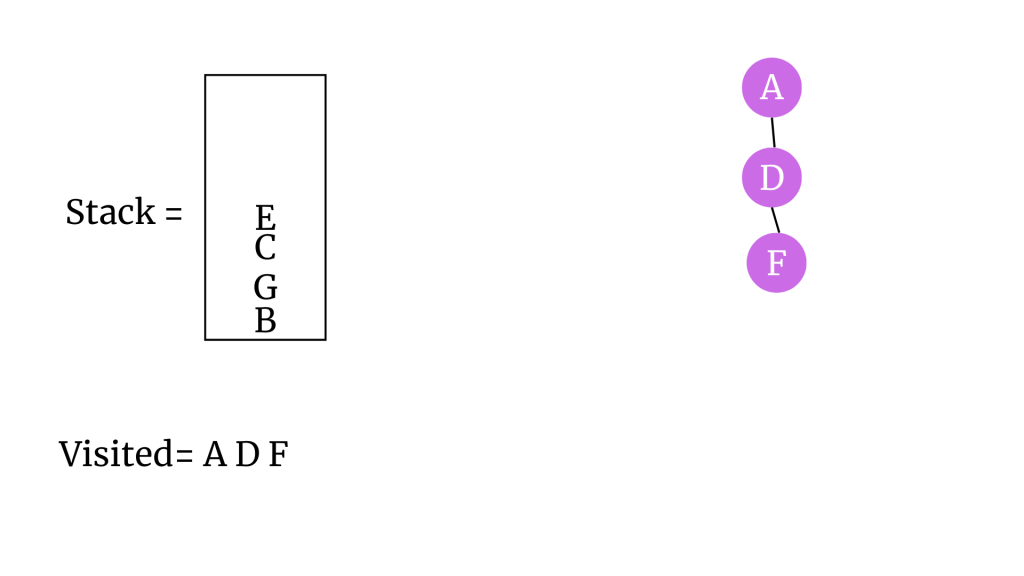
“E” vertex’inin komşusu olan K’yi stack’e ekleyelim. E’yi ziyaret edildi olarak işaretleyelim ve stack’ten çıkaralım. E’yi ağaca ekleyelim.
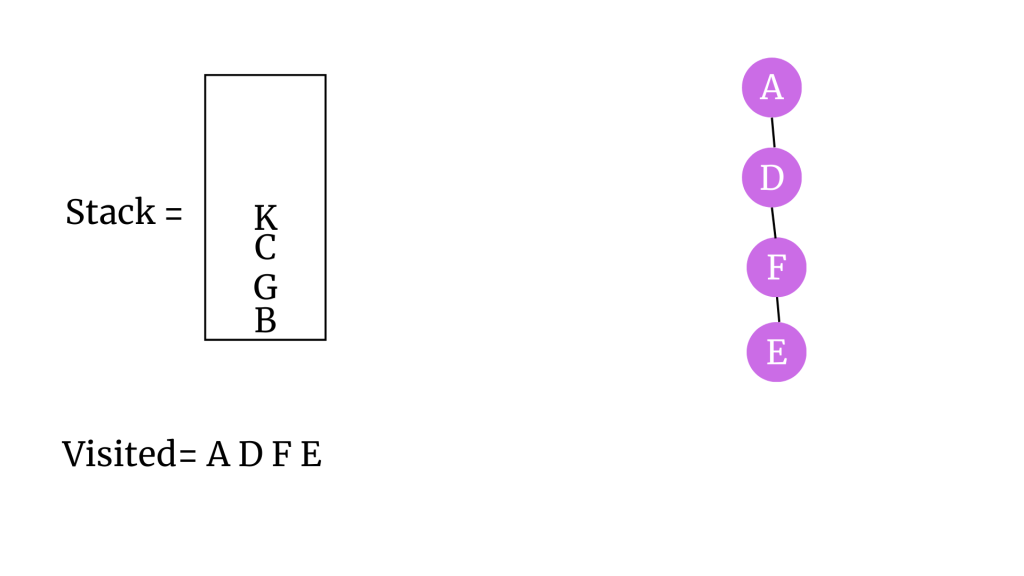
“K” vertex’inin komşusu olan H’yi stack’e ekleyelim. K’yi ziyaret edildi olarak işaretleyelim ve stack’ten çıkaralım. K’yi ağaca ekleyelim.
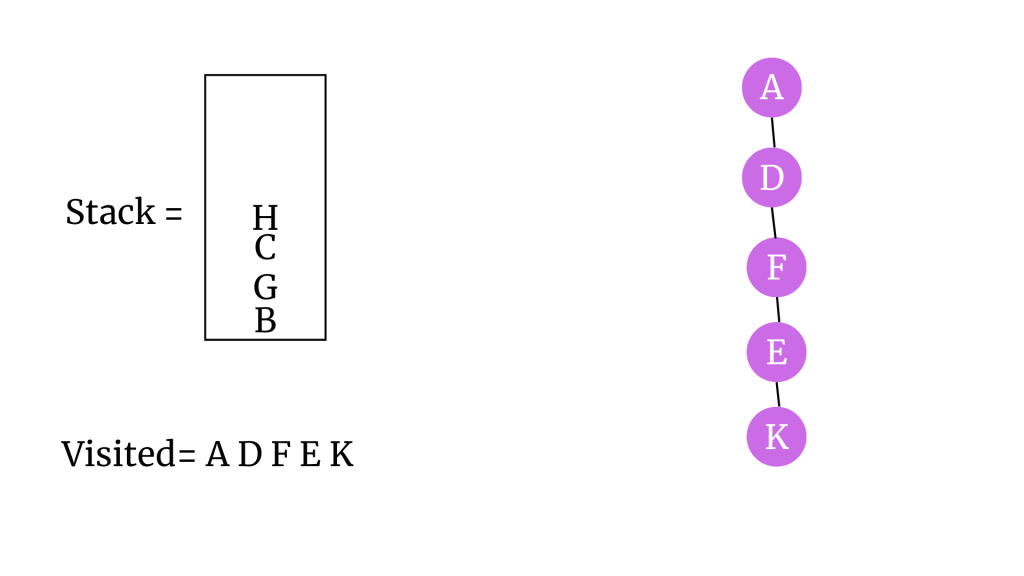
H vertex’inin tüm komşuları stack’te yer aldığı için komşuları tekrar stack’e eklenmeyecek. H’yi ziyaret edildi olarak işaretleyelim ve stack’ten çıkaralım. H’yi ağaca ekleyelim.
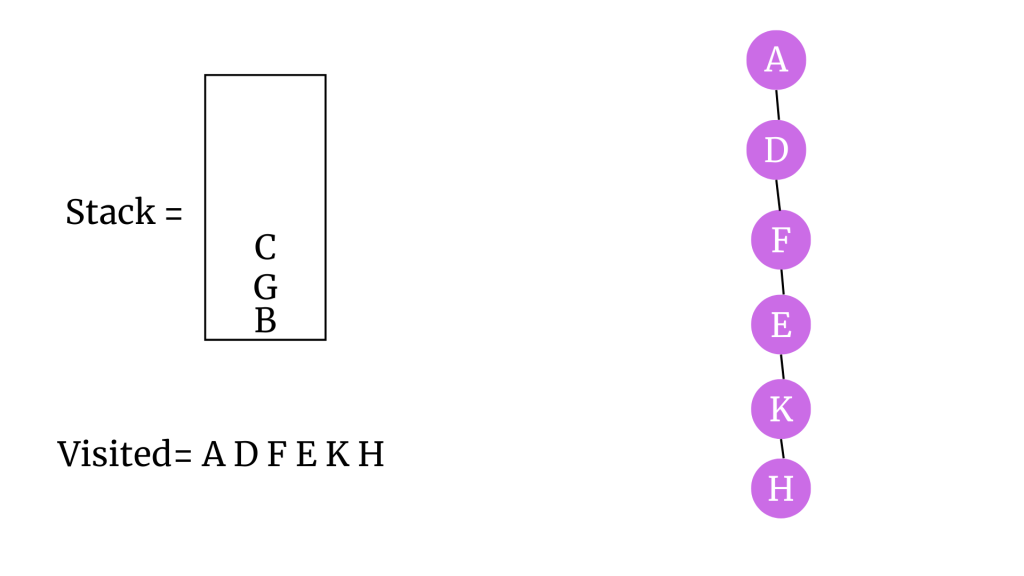
C’yi ziyaret edildi olarak işaretleyelim ve stack’ten çıkaralım. C’yi ağaca ekleyelim.

G’yi ziyaret edildi olarak işaretleyelim ve stack’ten çıkaralım. G’yi ağaca ekleyelim.
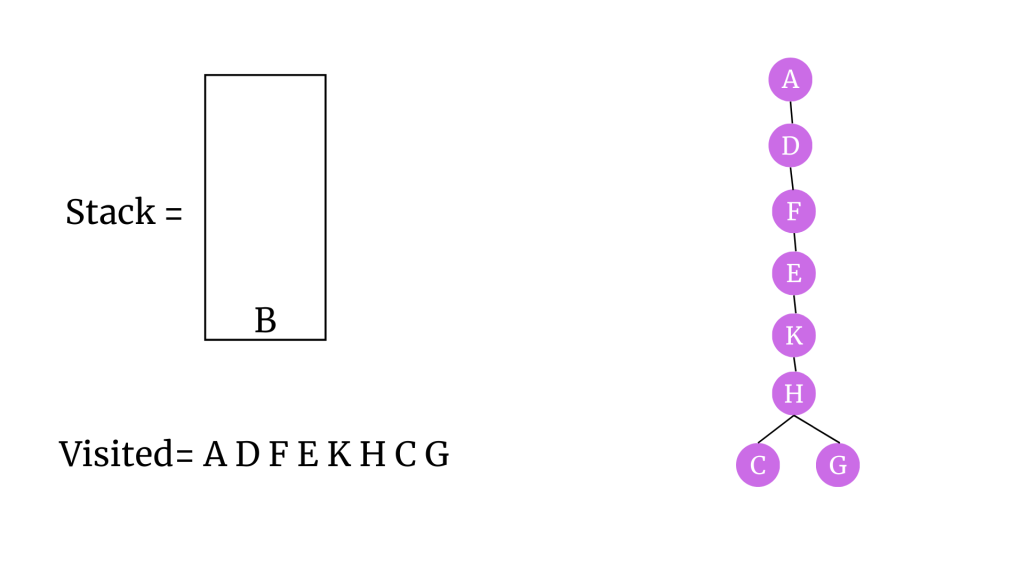
B’yi ziyaret edildi olarak işaretleyelim ve stack’ten çıkaralım. B’yi ağaca ekleyelim.
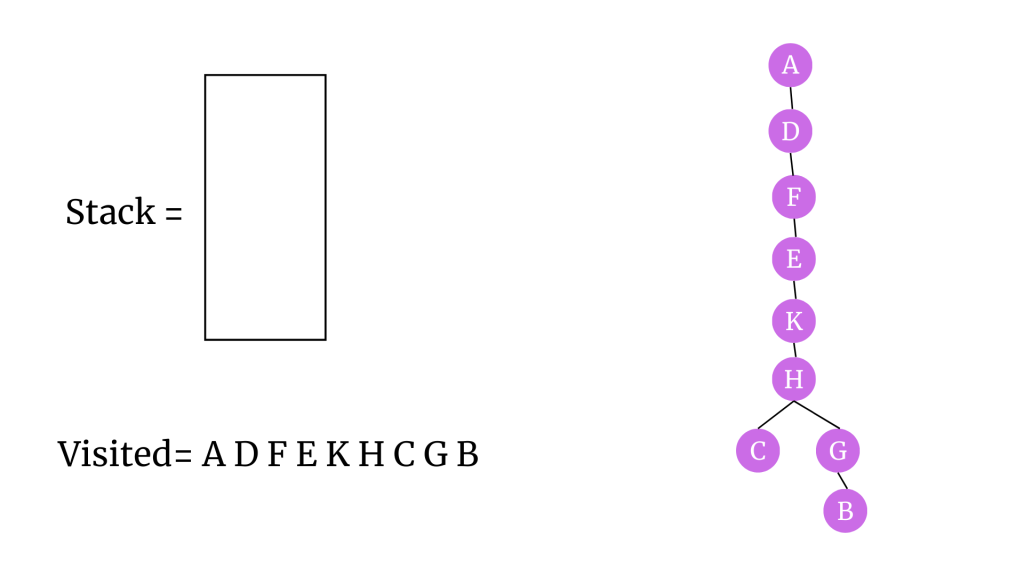
Tüm vertex’ler ziyaret edildi ve stack boşaltıldı. Böylece graph’da DFS ile gezinme işlemi tamamlandı.