Hiyerarşik bir yapı oluşturmak için kullanılan doğrusal olmayan bir veri yapısıdır.
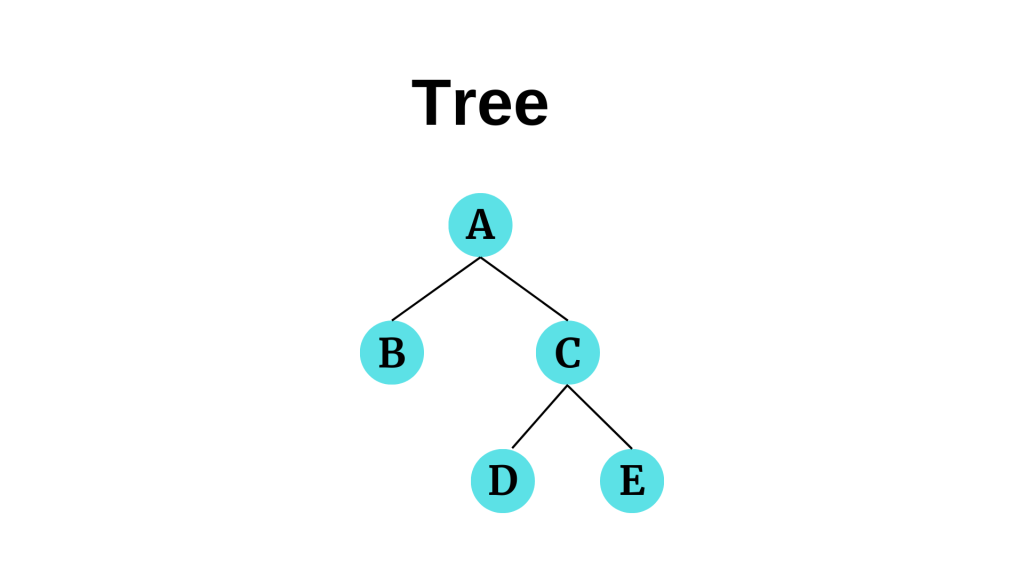
Ağaç veri yapısıyla ilgili bilmemiz gereken kavramlar:
- Node (Düğüm): Verilerin tutulduğu ağacın her bir elamanıdır.
- Root (Kök): Ağacın başlangıç node’udur.
- Child (Çocuk): Bir node’a doğrudan bağlı olan node’lardır.
- Parent (Ebeveyn): Bir node’un doğrudan bağlı olduğu node’dur.
- Sibling (Kardeş): Parent’ları aynı olan düğümlerdir.
- Ancestor (Ata): Bir node’dan köke kadar olan yoldaki node’un parent’ı hariç diğer nodelardır.
- Torun (Dedscendant): Bir node’un çocuklarına bağlı olan node’lardır.
- Leaf (Yaprak): Çocuğu olmayan nodelardır.
- Degree (Derece): Node’un çocuk sayısıdır.
- Depth (Derinlik): Bir node’un köke olan uzaklığıdır. Genellikle kök node’un derinliği “0” olarak kabul edilir.
- Height (Yükseklik): Bir node’un kendisiyle ilişkili en uzak leaf node’una olan uzaklığıdır. Leaf node’unun yükselikliği genellikle “0” kabul edilir.
- Path (Yol): Kök düğümden bir düğüme gidebilmek için izlenilmesi gereken node’ların listesidir.
Aşağıdaki ağaçta her bir node için; node’ların “çocuklarını”, “ebeveynlerini”, “kardeşlerini”, “derecelerini”, “yüksekliklerini” ve “derinliklerini” inceleyelim.
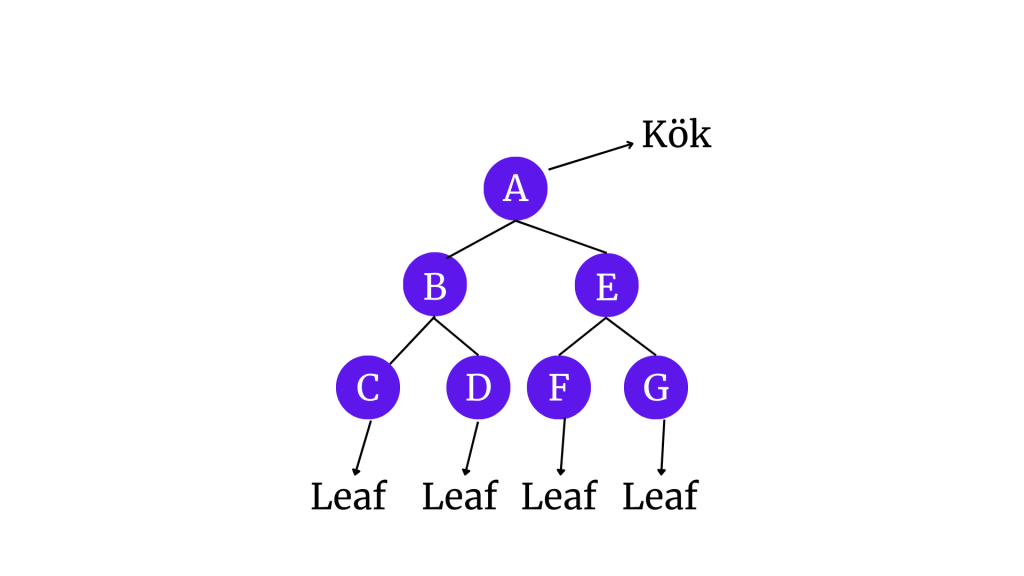
| A (Kök) | B | C | D | E | F | G | |
| Parent | Yok | A | B | B | A | E | E |
| Child | B, E | C, D | Yok | Yok | F, G | Yok | Yok |
| Sibling | Yok | E | D | C | B | G | F |
| Degree | 2 | 2 | 0 | 0 | 2 | 0 | 0 |
| Depth | 0 | 1 | 2 | 2 | 1 | 2 | 2 |
| Height | 2 | 1 | 0 | 0 | 1 | 0 | 0 |
Ağaçların Özellikleri
- Doğrusal olmayan (non-linear) veri yapısına sahiptirler.
- Hiyerarşik bir yapıya sahiptirler.
- Diğer veri yapılarında olduğu gibi eleman ekleme, silme, gezinme işlemleri yapılabilmektedir.
- Linked list mantığında kodlanırlar.
- Node’ların birden fazla çocuğu olabilirken, kök (0) hariç ebeveynleri 1 tanedir.
- Her node’a tek bir yoldan ulaşılabilir.
- Her ağaç aynı zamanda bir graphtır.
- Ağaçlarda, graphlarda olduğu gibi cycle durumu gözlenmez.
- En yaygın kullanılan ağaç “binary tree” dir.
Ağaç Türleri
- Binary Tree (İkili Ağaç)
- Binary Search Tree (İkili Arama Ağacı)
- Balanced Search Tree (Dengeli Arama Ağacı)
- AVL Tree
- Splay Tree
- Red – Black Tree
- B Tree
- Coding Tree
- Dictionary Tree
- Heap Tree
- Expression Tree